DDS（Direct Digital Synthesizer）を応用した任意サイクルの生成

FPGAに実装するタイマ回路など同期設計で任意サイクルを使用したいとき、ベースクロックから任意サイクルのイネーブル信号を生成する回路を使います。ここではその任意サイクルを生成するためのパラメータを計算できます。

なお本回路はベースクロック信号の精度に依存するため、イネーブル信号の精度を完全に保証するものではありませんのでご了承ください。 ~~てい倍はできません~~逓倍のパラメータも出せるみたいです。

モード＝	分周逓倍
ベースクロック＝	Hz
ターゲットサイクル＝	サイクル
カウンタ最大ビット幅＝	bit 計算するカウンタのビット幅が大きいほど精度が良くなります。誤差が0になればそこで計算を打ち切ります。
HDL出力：	VerilogHDL VHDL SFL+

log：

計算結果：許容できる誤差のビット幅を選択してください。

HDL出力：

解説

分周モードについて

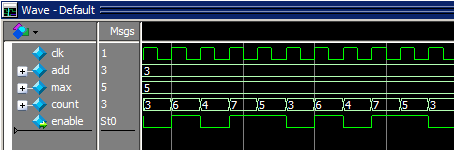
DDSを応用したカウンタでベースクロックから任意サイクルのイネーブル信号を生成します。特徴はイネーブル信号が偏っていないことです。 FPGAでの同期設計のときに任意サイクル生成回路として使用します。非同期回路じゃなくてよい場合はこういう手もあるかなと。

例えば簡単な例だと、ベースクロック50MHzでターゲットサイクルが30MHzであれば、その比は5:3なので、パラメータはそれぞれ加算値3、最大値5となります。

以下は疑似コードです。

circuit DDS_5to3
{
	input rst, clk;
	output enable;

	wire add = 3; // 加算値
	wire max = 5; // 最大値
	reg count;

	if(clk){
		if(rst){
			count = 0;
		}
		else if(count < max){
			count += add;
		}
		else{
			count += add - max;
			enable();
		}
	}
}

５クロックに３回enable信号がHiになります。これは簡単ですね。あくまでイネーブル信号であり、30MHzのクロックではないことに注意してください。

違う例では、ベースクロック50MHzでターゲットサイクルが33.8688MHz（PlayStationのCPU周波数）だと、最大公約数が3200です。それぞれ最大公約数で割ると、加算値10584、最大値15625となります。これは12bitのカウンタを使うことで誤差が0となり、最大公約数が大きいほどカウンタのビット幅が少なくて済むわけです（ここでの誤差とは、理想的なターゲット周波数と実際のイネーブルサイクルの差）。

では最大公約数が小さい場合どうしましょうか？もちろんカウンタのbit幅を増やせば増やすほど誤差は小さくなります。ただし、誤差は小さくしたいけど、カウンタのビット幅もできるだけ小さくしたい。そこで適切な加算値と最大値をパラメータとして見つける必要があります。

例えばファミコンの描画プロセッサの動作周波数は5.369318MHzです。これをベースクロック50MHzから生成するとなると、パラメータ探索結果は以下の通り。

	カウンタ 5bit  加算値=      1  最大値=       9  誤差=+186237.55555555596947669983
	カウンタ 6bit  加算値=      3  最大値=      28  誤差= -12175.14285714272409677505
	カウンタ 8bit  加算値=     13  最大値=     121  誤差=  +2582.82644628081470727921
	カウンタ 9bit  加算値=     16  最大値=     149  誤差=   -190.48322147689759731293
	カウンタ11bit  加算値=    109  最大値=    1015  誤差=   +140.12807881738990545273
	カウンタ12bit  加算値=    189  最大値=    1760  誤差=     +0.18181818164885044098
	カウンタ18bit  加算値=  14002  最大値=  130389  誤差=     -0.03606132417917251587
	カウンタ19bit  加算値=  16837  最大値=  156789  誤差=     +0.00062504410743713379
	カウンタ20bit  加算値=  50322  最大値=  468607  誤差=     -0.00005548354238271713
	カウンタ22bit  加算値= 218125  最大値= 2031217  誤差=     -0.00000295415520668030
	カウンタ24bit  加算値= 822178  最大値= 7656261  誤差=     +0.00000026077032089233
	カウンタ26bit  加算値=2684659  最大値=25000000  誤差=      0.00000000000000000000

結果、カウンタが26bitあれば誤差0のイネーブルサイクルが作れます。ただ、（ベースクロック自体の誤差から見て十分小さい誤差かどうか判断して）誤差をいくらか許容するならば、カウンタ18bitあたりの加算値と最大値を選択することで、レジスタ数と回路規模を抑制することができます。

また、ここで誤差のプラスはターゲットサイクルに対し速いサイクルが、マイナスは遅いサイクルが生成されることを意味します。動作期間が決まっている場合、遅いサイクルだと間に合わなくなることがあるため、速いサイクルを使用する方が良いようです。

逓倍モードについて

PLLのIPを使用するとき、IPジェネレータでターゲット周波数を指定するかと思います。場合によって分周・逓倍のパラメータが不明な場合に、この計算機の「逓倍モード」でターゲットサイクルを指定すればパラメータが分かります。なんか同じロジックで動いたので追加しました。

例えば、27MHzからHDMI用に124.875MHzを生成したくPLLを生成したとき、タイミング制約で指定する -multiply_by と -divide_by の値が必要です。パラメータ探索結果は以下の通り。

	出力周波数=108000000Hz Mul= 4 Div=1 誤差=-16875000.000000
	出力周波数=135000000Hz Mul= 5 Div=1 誤差=+10125000.000000
	出力周波数=121500000Hz Mul= 9 Div=2 誤差= -3375000.000000
	出力周波数=126000000Hz Mul=14 Div=3 誤差= +1125000.000000
	出力周波数=124200000Hz Mul=23 Div=5 誤差=  -675000.000000
	出力周波数=124875000Hz Mul=37 Div=8 誤差=        0.000000

Mul=37 Div=8 が分かりました。まぁ、入出力周波数をそれぞれ最大公約数3375000で割れば出てくるんですけどね。あと大抵、IPジェネレータが生成したファイルに書かれてます。

// _COMMENT_

%d COUNT_WIDTH _COUNT_WIDTH_

circuit DDS_sflp
{
	instrout enable;

	sel add<COUNT_WIDTH>;
	sel max<COUNT_WIDTH>;
	reg_wr count<COUNT_WIDTH>;
	sel sa<COUNT_WIDTH>;

	add = _ADD_NUM_;
	max = _MAX_NUM_;

	sa = count - max;

	if(sa<COUNT_WIDTH-1>){ // count < max
		count += add;
	}
	else{
		count := sa + add;
		enable();
	}
}

// _COMMENT_

module DDS_verilog (
	input wire rst;
	input wire clk;
	output wire enable;
);
	localparam COUNT_WIDTH = _COUNT_WIDTH_;

	wire [COUNT_WIDTH-1:0] add;
	wire [COUNT_WIDTH-1:0] max;
	reg  [COUNT_WIDTH-1:0] count;
	wire [COUNT_WIDTH-1:0] sa;

	assign add = COUNT_WIDTH'd_ADD_NUM_;
	assign max = COUNT_WIDTH'd_MAX_NUM_;

	assign sa = count - max;

	always @(posedge clk) begin
		if(rst)
			count <= COUNT_WIDTH'd0;
		else if(sa[COUNT_WIDTH-1]) // count < max
			count <= count + add;
		else
			count <= sa + add;
	end

	assign enable = ~sa[COUNT_WIDTH-1];

endmodule

-- _COMMENT_

library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_unsigned.all;
use ieee.numeric_std.all;

entity DDS_vhdl is
	port(
		rst, clk : in std_logic;
		enable : out std_logic
	);
end DDS_vhdl;

architecture RTL of DDS_vhdl is

constant COUNT_WIDTH : integer := _COUNT_WIDTH_;
constant ADD_NUM : std_logic_vector(COUNT_WIDTH-1 downto 0)
	:= std_logic_vector(to_unsigned(_ADD_NUM_, COUNT_WIDTH));
constant MAX_NUM : std_logic_vector(COUNT_WIDTH-1 downto 0)
	:= std_logic_vector(to_unsigned(_MAX_NUM_, COUNT_WIDTH));

signal add   : std_logic_vector(COUNT_WIDTH-1 downto 0);
signal max   : std_logic_vector(COUNT_WIDTH-1 downto 0);
signal count : std_logic_vector(COUNT_WIDTH-1 downto 0);
signal sa    : std_logic_vector(COUNT_WIDTH-1 downto 0);

begin

	add <= ADD_NUM;
	max <= MAX_NUM;

	sa <= count - max;

	process(clk) begin
		if rising_edge(clk) then
			if rst='1' then
				count <= (others => '0');
			elsif sa(COUNT_WIDTH-1)='1' then -- count < max
				count <= count + add;
			else
				count <= sa + add;
			end if;
		end if;
	end process;

	enable <= not sa(COUNT_WIDTH-1);

end RTL;